前 言
空间重构也叫折纸盒,常考的空间重构一般为六面体。本文将讲解六面体中最常用的解题方法,即相对面、相邻面等,以此帮助大家解决空间类的题目。
考点一:相对面
在六面体中,相对着的两个面即为相对面。如果某两个面是相对面,则在六面体只能看到3个面的情况下,这两个相对面只能出现一个面,并且必须出现一个面。在实际解题中, 如果立体图形有一组相对面同时出现的选项,可以直接排除。
在六面体的平面展开图中,相对面基本判定法则有2种:
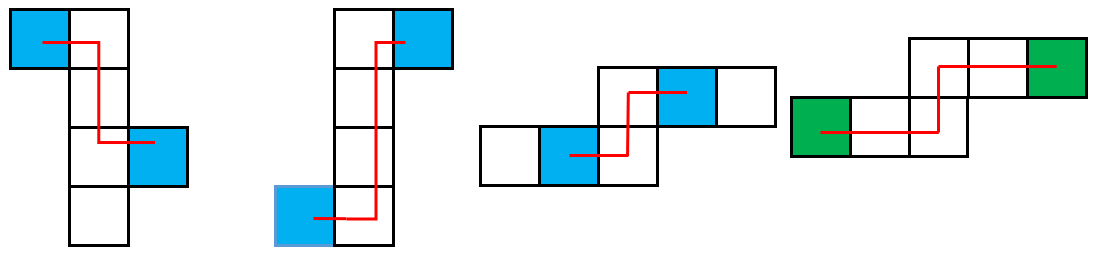
(1)同行或同列相隔一个面:在一个展开图中,在同一行或者同一列的面,并且两个面中间隔一个面,那么这两个面就是相对面。如图1所示,两个绿色面为同列中间隔了一个面,二者为相对面;两个黄色面为同列中间隔了一个面,二者为相对面;两个蓝色面为同行中间隔了一个面,二者为相对面。

(2)如果两个面在“Z”字形两端,并且紧靠着“Z”字形中间的那条线,那么这两个面就是相对面。图1-3中,两个蓝色面均在“Z”字形两端,并且均紧邻“Z”字形中间的那条线,所以,3组蓝色面均为相对面。图4中,2个绿色面虽然也在“Z”字形两端,但没有紧邻“Z”字形中间的那条线,所以,两个绿色的面不是相对面。
★
题目示例
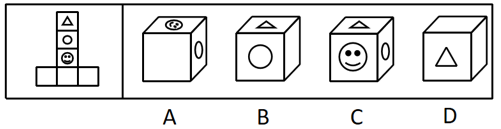
左边给定的是正方体的外表面展开图,右边哪一项不能由它折叠而成?
【解析】
将展开图标上序号如下图,逐一进行分析。
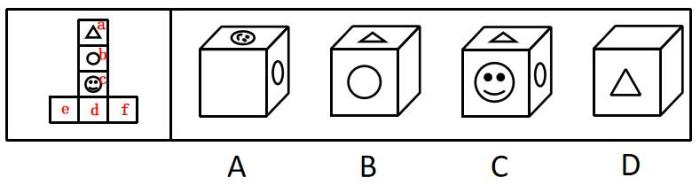
A项:选项由面b、面c与面f构成,选项与展开图一致,排除;
B项:选项由面a、面b与面f构成,选项与展开图一致,排除;
C项:选项由面a、面b与面c构成,展开图中面a和面c为相对面,不能同时出现,选项与展开图不一致,当选;
D项:选项由面a、面d与面f构成,选项与展开图一致,排除。
本题为选非题,故正确答案为C。
考点二:相邻面
在六面体中,当出现图形指向性明显的面时,因为图形折叠前后的相对位置保持不变,所以可以优先考虑相对位置。在六面体的平面展开图中,图形指向性明显的面大致如下图,根据指向性明显的面观察在立体图中的位置关系,判断与展开图中位置关系是否一致,若不一致,则不能由题干展开图折叠而成。
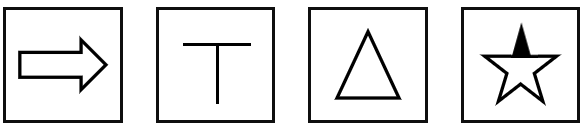
在六面体中,相邻的两个面共用一条边,我们叫公共边。公共边的判断方法有两个:
1.平面图中构成直角的两个边是同一条边,如蓝线所示:
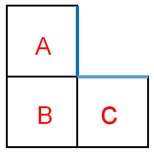
2.四面共线,首尾的两条边是同一条边,如蓝线所示:
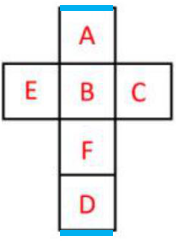
因为相邻面在折叠前后相邻关系保持不变,可以从公共边来确定图形的相对位置。利用相对位置可以解决很多空间重构题目,但图形看上去会比较难辨别其相对位置,提醒大家可以利用标记辅助做题,根据公共边的特点去判断图形的相对位置,会更加直观清晰,从而排除错误选项。
★
题目示例
左边给定的是正方体的表面展开图,下列哪一项是由它折叠而成的?
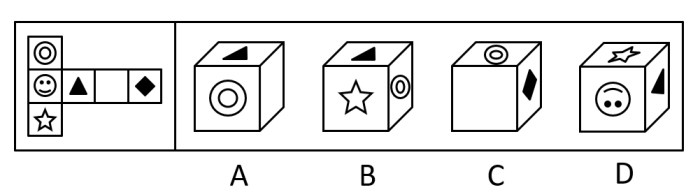
【解析】
本题为空间重构类题目。
A项:展开图中三角形底边所对的面是五角形,选项中三角形底边所对的面为圆环,选项与题干不一致,排除;
B项:展开图中五角星头顶所对的面是笑脸,选项中五角星头顶所对的面为三角形,选项与题干不一致,排除;
C项:选项与题干一致,当选;
D项:展开图中三角形头顶所对的面是圆环,选项中三角形头顶所对的面为笑脸,选项与题干不一致,排除。
故正确答案为C。
小粉笔tips
画边法可以解决绝大部分的六面体的题目,具体方法为:
第一步:结合选项,找到一个特殊面中的唯一点,即明确位置的点;
第二步:在展开图和立体图中,以唯一点为起点出发,分别按顺(逆)时针方向画边并标号;
第三步:展开图和立体图进行匹配,如果相对应的面不一致,排除错误选项。
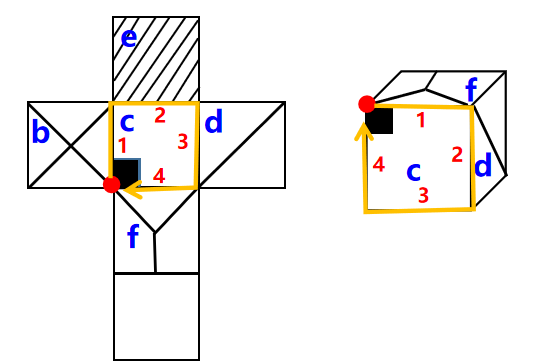
分析:如上图所示,结合展开图和立体图,选择带有黑色小正方形的c面作为确定的特殊面进行画边,将黑色直角顶点作为唯一点,在展开图和立体图中均顺时针画边并标出序号。观察可知,在展开图中,边1和“b”面相邻,但在立体图中,边1和“f”面相邻,二者不对应,所以该立体图不能由左侧的展开图折叠而成,可以排除。
★
题目示例
左边给定的是纸盒外表面的展开图,右边哪一项能由它折叠而成?请把它找出来。
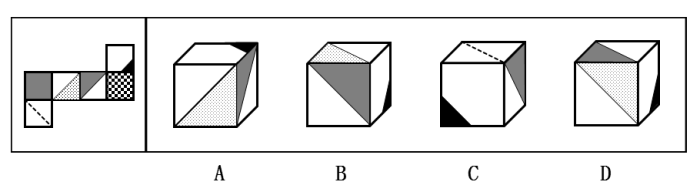
【解析】
本题考查六面体的空间重构。观察发现,选项中的立体图形都包含灰色三角形所在的面。可以通过画边法解答。以灰色三角形的直角为出发,顺时针依次标出各边,如图1所示:
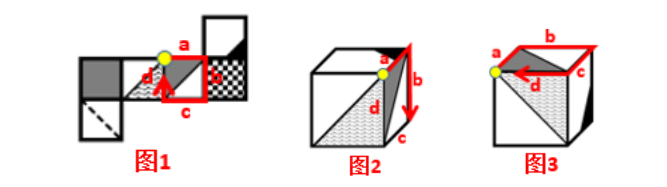
A项:题干中a边挨着黑三角形所在面的空白边,与黑三角形没有公共边,而选项中a边与黑三角形有公共边(如图2所示),排除;
C项:题干中黑三角形所在的面与虚线所在的面是相对面,而选项是相邻面,排除;
D项:题干中a边挨着黑三角所在的面(如图1所示),而选项中c边挨着黑三角所在的面(如图3所示),排除;
故正确答案为B。