特征数列是数字推理的重要组成部分,主要考查分数数列、多重数列、幂次数列以及图形数阵。特征数列有比较明显的特征,做题的时候稍加认真分析就能辨别出来。小粉笔今天就带着大家从考试的角度梳理下特征数列的高频考点!
考点一:分数数列
(一)题型特征
数列中全部是或者大部分数是分数
(二)解题思路
①观察分子、分母是否具备递增或者递减的趋势;
②若否,通过反约分把数列转化为分子、分母单调递增或递减的趋势;
③分子、分母单独成规律或者分子、分母结合在一起成规律。
题目示例
例:1/2,3/4,5/8,7/16,9/32,( )
A.13/42
B.11/48
C.13/55
D.11/64
【解析】
观察数列,分子、分母均具备递增的趋势。先看分子,1、3、5、7、9、( )是公差为2的等差数列,则所求分子=9+2=11;再看分母,2、4、8、16、32、( )是公比为2的等比数列,则所求分母=32×2=64;故所求项为11/64。正确答案为D选项。
考点二:多重数列
(一)题型特征
数列中项数较多(≥7项,包含所求项)
(二)解题思路
①交叉分组:将原数列拆分为奇数项和偶数项,分别查找规律。
②相邻两两或三三分组:将原数列两两或三三分组,分组后通过简单计算后查找规律。
题目示例
例:1,1,2,3,4,4,6,5,( ),( )
A.4,6
B.4,9
C.5,6
D.5,9
【解析】
观察数列,发现所给项数较多,优先考虑多重数列,交叉分组无规律,考虑两两分组。(1, 1)、(2, 3)、(4,4)、(6, 5)、(( ),( )),组内之和分别为2、5、8、11、( ),是公差为3的等差数列,则最后所求两项之和为11+3=14,只有D项符合,故正确答案为D选项。
考点三:幂次数列
(一)题型特征
①数列各项本身是幂次数(普通幂次)
②数列各项附近有幂次数(修正幂次)
(二)解题思路
①普通幂次:直接转化为幂次数查找规律
②修正幂次:转化为幂次数±修正项,进而查找规律
题目示例
例: 1, 8,27,64, 125,( )
A.196
B.216
C.225
D.289
【解析】
观察数列,发现原数列各数依次转化为13,23,33,43,53,( ),则所求项为63=216,故正确答案为B选项。
考点四:图形数阵
(一)题型特征
有图也有数,图形多为无心圆或者有心圆
(二)解题思路
①无心圆:横向、纵向或对角线交叉找规律
②有心圆:凑中心
题目示例
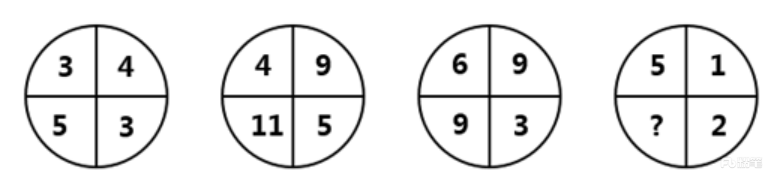
A.8 B.9 C.10 D.11
【解析】有图有数为图形数阵,观察数列发现:
第一个数阵中,3×3=4+5;
第二个数阵中,4×5=9+11;
第三个数阵中,6×3=9+9;
因此,第四个数阵中应该满足:5×2=1+所求项,可知所求项为9。
故正确答案为B。
数字推理中特征数列的考点就带小伙伴们了解到这喽,想要了解更多特征数列的知识点,快来粉笔和老师们一起学习吧!