容斥原理问题属于数学运算中的经典题型,并且容斥原理问题的解题方法比较简单,难度较低,属于套路化的题目,是学习起来性价比比较高的题型,建议考生优先学习。
容斥原理问题常见的命题形式分为两集合容斥原理和三集合容斥原理,除利用公式外,部分题目还需要利用画图法解题。
01
两集合容斥原理
(一)必备基础知识
1.题型特征
题干中涉及两个集合,各集合之间出现交叉重叠。
2.基本公式
A + B - A∩B = 总数 - 都不。
(二)典型考法及解题思路
例
(2018国考)
某乡有32户果农,其中有26户种了柚子树,有24户种了橘子树,还有5户既没有种柚子树也没有种橘子树,那么该乡同时种植柚子树和橘子树的果农有:
A.23户
B.22户
C.21户
D.24户
【思路梳理】
题目中涉及两个集合,且各集合之间出现交叉重叠,判定本题为容斥原理问题;题目中分别给出了两个集合各自的数量和两个集合完全不相交部分的数量,判定本题可以利用两集合容斥原理公式计算。可以将题目中所给的数据代入两集合容斥原理公式中,即可求出同时种植柚子树和橘子树的果农数量。
解题步骤:
根据两集合容斥原理基本公式A + B - A∩B = 总数 - 都不,可知在本题中,种柚子树的户数+种桔子树的户数-同时种植柚子树和橘子树的户数=总户数-既没有种柚子树也没有种橘子树的户数,代入题目数据,可得26+24-同时种植柚子树和橘子树的户数=32-5,解得同时种植柚子树和橘子树的有23户。故正确答案为A。
(三)粉笔小拓展
对于两集合容斥原理问题考查的相对较少,主要考查基本公式的应用,直接根据公式代入数据求解即可。
02
三集合容斥原理
(一)必备知识
1.题型特征
题干中涉及三个集合,各集合之间出现交叉重叠。
2.基本公式
(1)标准型公式
①使用条件:题干中涉及三个集合,各集合之间出现交叉重叠,其中给出A∩B、A∩C和B∩C的数值。
②公式:A + B + C - A∩B - A∩C - B∩C + A∩B∩C = 总数 - 都不。
(2)非标准型公式
①使用条件:题干中涉及三个集合,各集合之间出现交叉重叠,其中给出“只满足两项”和“满足三项”的数值。
②公式:A + B + C - 满足两项 - 满足三项×2 = 总数 - 都不。
注:非标准型公式中的“满足两项”是指“只满足两项”,要和“满足两项及以上”做好区分。
(3)常识型公式
①使用条件:题干中涉及三个集合,各集合之间出现交叉重叠,其中给出“只满足两项”和“满足三项”的数值,求“只满足一项”的数值,或出现“人次数”、“买门票”这类字眼。
②公式:满足一项 + 满足两项 + 满足三项 = 总数 - 都不。
(二)典型考法与解题思路
例
(2018四川)
针对100名旅游爱好者进行调查发现,28人喜欢泰山,30人喜欢华山,42人喜欢黄山,8人既喜欢黄山又喜欢华山,10人既喜欢泰山又喜欢黄山,5人既喜欢华山又喜欢泰山,3人喜欢这三个景点,则不喜欢这三个景点中任何一个的有多少人:
A.20
B.18
C.17
D.15
E.14
F.13
G.12
H.10
【思路梳理】
题干中涉及三个集合,且各集合之间出现交叉重叠,判定本题为容斥原理问题;题目中分别给出了三个集合两两重叠部分和三个集合都重叠部分的数值,判定本题可以利用三集合容斥原理标准型公式计算。可以将题目中所给的数据代入三集合容斥原理标准型公式中,即可求出三个景点都不喜欢的人数。
解题步骤:
根据三集合容斥原理标准型公式A + B + C - A∩B - A∩C - B∩C + A∩B∩C = 总数 - 都不,可知在本题中,28+30+42-8-10-5+3=100-三个景点都不喜欢的人数,解得三个景点都不喜欢的人数为20。故正确答案为A。
例
(2019国考)
某乡镇举行运动会,共有长跑、跳远和短跑三个项目。参加长跑的有49人,参加跳远的有36人,参加短跑的有28人,其中只参加两个项目的有13人,参加全部项目的有9人。那么参加该次运动会的总人数为多少:
A.75
B.82
C.88
D.95
【思路梳理】
题干中涉及三个集合,且各集合之间出现交叉重叠,判定本题为容斥原理问题;题目中分别给出了“只满足两项”和“满足三项”的数值,判定本题可以利用三集合容斥原理非标准型公式计算。可以将题目中所给的数据代入三集合容斥原理非标准型公式中,即可求出参加该次运动会的总人数。在列式求解的过程中,注意题目所求为“参加该次运动会的总人数”,因此“都不”=0。
解题步骤:
根据三集合容斥原理非标准型公式A + B + C - 满足两项 - 满足三项×2 = 总数 - 都不,可知在本题中,49+36+28-13-2×9=参加该次运动会的总人数,解得参加该次运动会的总人数为82。故正确答案为B。
例
(2017重庆选调)
一项农村家庭的调查显示,电冰箱拥有率为49%,电视机拥有率为85%,洗衣机拥有率为44%,至少有两种电器的占63%,三种电器齐全的占25%,则一种电器都没有的比例为:
A.10%
B.15%
C.20%
D.25%
【思路梳理】
题干中涉及三个集合,且各集合之间出现交叉重叠,判定本题为容斥原理问题;题目中分别给出了“至少满足两项”和“满足三项”的数值,进而可以求出“只满足两项”的数值,判定本题可以利用三集合容斥原理非标准型公式计算。可以将题目中所给的数据代入三集合容斥原理非标准型公式中,即可求出一种电器都没有的比例。列式求解的过程中需要注意,因为题目给出的数据都是拥有率,所以公式中“总数”对应部分应为所有人都拥有,即100%;另外,“至少满足两项”对应的数值既包含“只满足两项”,又包含“满足三项”,即至少满足两项=只满足两项+满足三项。
解题步骤:
因为“至少满足两项=只满足两项+满足三项”,可得只拥有两种电器的比例=至少有两种电器的比例-三种电器齐全的比例=63%-25%=38%,根据三集合容斥原理非标准型公式A + B + C - 满足两项 - 满足三项×2 = 总数 - 都不,可知在本题中,49%+85%+44%-38%-2×25%=100%-一种电器都没有的比例,解得一种电器都没有的比例为10%。故正确答案为A。
(三)粉笔小拓展
三集合容斥原理问题的计算难度一般都不会太高,且在计算时,只要选项尾数不同,均可结合尾数法计算,若遇到例2这类选项尾数有相同的情况,也可以结合选项的设置有选择地使用尾数法,比如例2在计算时可以选择先用尾数法,在确定尾数为0之后再去精确计算,这样假如尾数不为0的话,利用尾数法已经可以锁定答案。常识型公式在实际题目中很少单独出现,一般都结合其他公式一起考查。
03
给具体单位型
(一)必备基础知识
1.题型特征
题干中涉及多个集合,各集合之间出现交叉重叠,且出现“只满足”某一条件,无法使用公式或者使用公式很麻烦。
2.解题思路
(1)根据题意画出交叉的两个或三个圈,代表各集合,在相应位置标上数字,一般从最中间开始标记,逐层向外,避免重复。
(2)每个封闭区域只标记一个数。
(二)典型考法与解题思路
例
(2016河南)
某公司组织歌舞比赛,共68人参赛。其中,参加舞蹈比赛的有12人,参加歌唱比赛的有18人,45个人什么比赛都没有参加。问其中参加歌唱比赛但不参加舞蹈比赛的有多少人?
A.9
B.11
C.15
D.17
【思路梳理】
题干中涉及两个集合,且各集合之间出现交叉重叠,判定本题为容斥原理问题;题目所求为“只满足”某一条件的数值,使用公式比较麻烦,因此判定本题可以利用画图法解题。先将题目代入两集合容斥原理公式求出两个集合重叠部分的数值,再利用画图法解题,根据题意画出交叉的两个圆代表两个集合,在相应位置标上数据,从中间重叠部分开始标记,逐层向外,即可求出参加歌唱比赛但不参加舞蹈比赛的人数。
解题步骤:
根据两集合容斥原理基本公式A + B - A∩B = 总数 - 都不,可知在本题中,参加舞蹈比赛的人数+参加唱歌比赛的人数-两种比赛都参加的人数=总人数-什么比赛都不参加的人数,代入题目数据,可得12+18-两种比赛都参加的人数=68-45,解得两种比赛都参加的人数为7;根据题意画图如下:
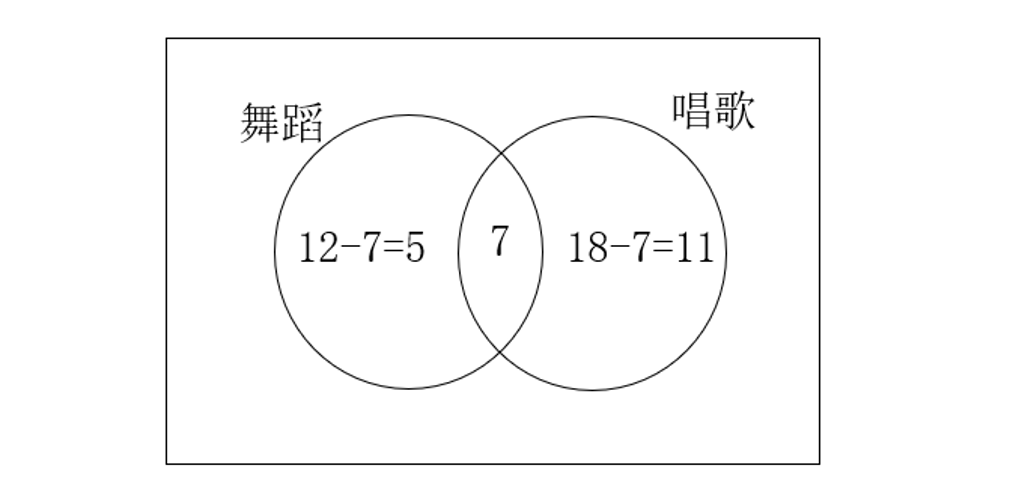
则题目所求参加歌唱比赛但不参加舞蹈比赛的人数=18-7=11人。故正确答案为B。
例
(2018联考)
联欢会上,有24人吃冰激凌、30人吃蛋糕、38人吃水果,其中既吃冰激凌又吃蛋糕的有12人,既吃冰激凌又吃水果的有16人,既吃蛋糕又吃水果的有18人,三样都吃的则有6人。假设所有人都吃了东西,那么只吃一样东西的人数是多少?
A.12
B.18
C.24
D.32
【思路梳理】
题干中涉及三个集合,且各集合之间出现交叉重叠,判定本题为容斥原理问题;题目所求为“只满足”某一条件的数值,使用公式很麻烦,因此判定本题可以利用画图法解题。根据题意画出交叉的三个圆代表三个集合,在相应位置标上数据,从中间重叠部分开始标记,逐层向外,注意去重,先分别求出只满足两项的人数,即可进一步求出只吃一样东西的人数;因为本题说明“所有人都吃了东西”,因此都不吃东西的人数为0,画图时无需特别画出外框区分不吃东西的人数。
解题步骤:
根据题意画图如下,共有24人吃冰激凌,三样都吃的有6人,既吃冰激凌又吃蛋糕的有12人,则只吃冰激凌和蛋糕的有12-6=6人;既吃冰激凌又吃水果的有16人,则只吃冰激凌和水果的有16-6=10人;既吃蛋糕又吃水果的有18人,则只吃蛋糕和水果的人有18-6=12人;则结合下图,只吃冰激凌的有24-6-6-10=2人,只吃蛋糕的有30-6-6-12=6人,只吃水果的有38-6-10-12=10人,题目所求只吃一样东西的人数为2+6+10=18。故正确答案为B。
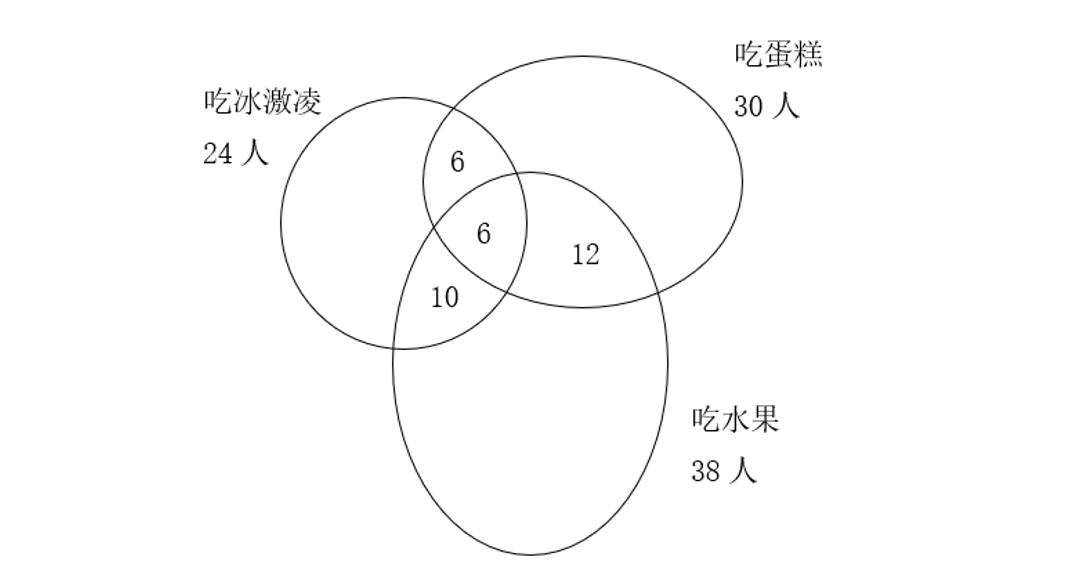
(三)粉笔小拓展
在实际做题过程中,部分题目虽然可以代入公式解题,但是如果利用画图法去分析,解题过程会更加清晰明了,特别是题目涉及“只满足某一个条件”的描述时,如例5利用公式也是可以计算的,但是假如题目条件更复杂一些的话就很容易混淆,而结合画图法分析却可以很轻松的捋顺各个条件之间的关系。
通过以上的分析,相信同学们对于容斥原理问题已经有了更深一步的了解,希望大家再接再厉,把容斥原理的公式和应用方法内化于心,并能够在做题时精准识别题型,对应合适的公式及方法,在考场上顺利拿分,取得理想的成绩,迎接新的人生旅途。
