比重问题是资料分析中的必考考点且考频很高,但题目难度往往不大。因此,对于考生而言,比重问题是性价比很高的题型,建议考生重点学习。
比重指部分在总体中所占的比率,有时也用贡献率、利润率等表述方式。它的题型特征主要是出现“占”字,计算时常用除法。常考题型有:
(1)现期比重。问现在的比重;
(2)基期比重。问过去的比重;
(3)两期比重。现期比重和基期比重作比较
必备公式
01
现期比重
(一)必备基础知识
1.题型特征
题目所求时间与材料时间一致,且出现“占”字,…占…的比重/…中,…所占的比重。
注:若题干未给出具体时间,且题干中出现“占”、“比重”等,则默认为所求时间与材料时间一致,即所求为现期比重。
2. 计算公式
比重=部分/总体=A/B*100%(A表示部分量、B表示总体量)
(1)A占B的比重;A(占前)是部分,B(占后)是总体。
(2)在B中,A所占的比重:类似倒装句,后面是部分,前面是总体。
3. 速算技巧
(1)截位直除法:较常用,但要注意判断选项间差距大小后再使用。
(2)特殊数字法:常用于“总体=部分/比重”中,其中比重为百分数,因此可将特殊百分数化成分数,使计算更简便,进而快速求解。
4. 解题思路
(1)已知部分和总体求比重:比重=部分/总体=A/B*100%(写的时候×100%可以不写)。
(2)已知部分和比重求总体:总体=部分/比重。
(3)已知总体和比重求部分:部分=总体×比重。
5. 概念引申
(1)增长贡献率=部分增长量/总体增长量,贡献率相当于比重,如问贡献率为多少时,直接求比重即可。
(2)利润率=利润/收入(资料分析)。资料分析中是宏观层面,是某行业或国家的真实数据,可能有税金、设备的折旧、人力成本、固定资产投资等有多重成本,为了方便计算,用利润/收入。
注:利润率=利润/成本(数量关系)。数量关系是理想化的模型,是小本买卖,不需要考虑实际情况。
(3)产销率=销量/产量,最后单位是%,可以看成比重。
(二)典型考法及解题思路
例
(2018国考)
2016年,全国城市公园数量排名前五的省份依次是广东、浙江、江苏、山东和云南,公园数量分别为3512个、1171个、942个、828个和683个。其中,广东省的公园面积达到65318公顷,占全国公园面积的比重超过17%;公园绿地面积达到89591公顷,占全国公园绿地面积的比重约为14%。
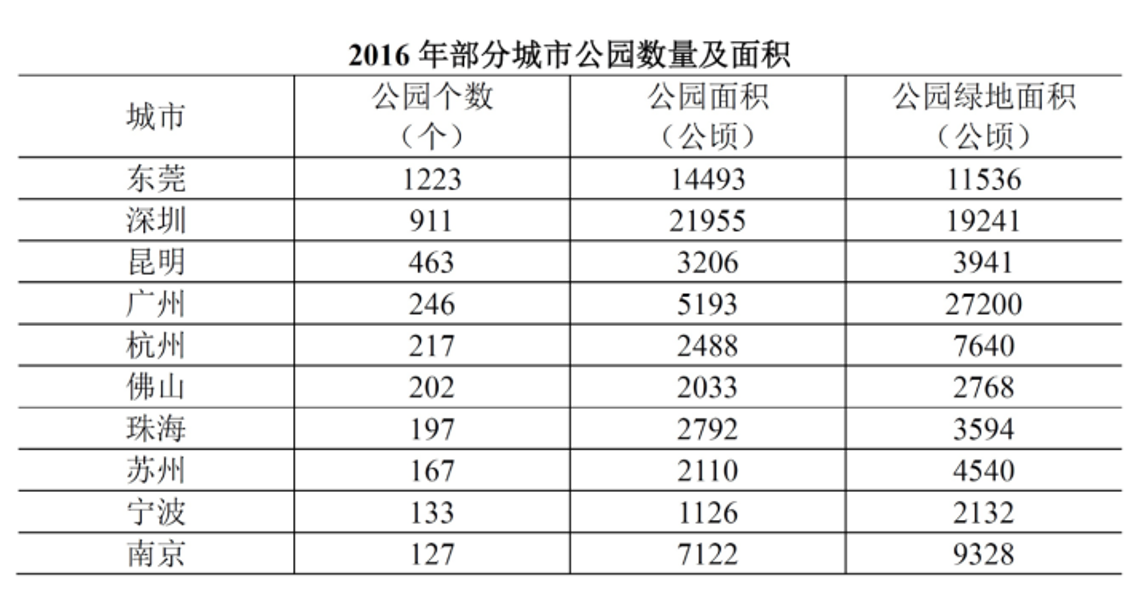
注:公园绿地指具有公园作用的所有绿地的统称,即公园性质的绿地,并非公园中的绿地面积,包括综合公园、专类公园、带状公园、街旁游乐园和社区公园等。
2016年,杭州公园数量约占浙江省公园总数的:
A. 19% B. 15% C. 27% D. 23%
【思路梳理】
由题干“2016年,…约占…的比重”,且材料时间也为2016年,可判定本题为现期比重问题。根据…占…的比重,占前为部分,占后为总体,可得杭州公园数量为部分量,浙江省公园总数为总体量,根据公式:比重=部分/总体,用杭州公园数量除以浙江省公园总数即可得出正确选项。
【解题步骤】
定位文字材料,浙江省公园数量1171个;定位表格材料,杭州公园数量217个,故比重=217/1171观察发现,选项间差距大,一步除法,只截分母,则原式约等于18.1%,最接近A选项19%。故正确答案为A。
例
(2019北京)
2016 年全国餐饮收入35799亿元,同比增长10.8%,餐饮收入占社会消费品零售总额的比重为10.8%。2016 年全社会餐饮业经营单位为365.5万个,同比下降8.2%;从业人数为1846.0万人,同比增长5.7%。
2016年社会消费品零售总额约为多少万亿元?
A.27 B.33 C.39 D.45
【思路梳理】
问题时间是2016年,材料时间是2016年,可判定所求时间为现期。定位文字材料发现,仅有“餐饮收入占社会消费品零售总额的比重为10.8%”与所求社会消费品零售总额相关,可判定本题为现期比重问题。由…占…的比重,占前为部分,占后为总体,可得餐饮收入为部分,所求社会消费品零售总额为总体,则本题可进一步梳理为已知部分和比重,求总体,代入公式求解即可。
解题步骤:
根据总体=部分/比重,可得社会消费品零售总额=35799/10.8%。
方法一:截位直除法。观察发现,选项差距大,一步除法,分母截两位计算,转化为 35799/11,首位商3,次位商2,与B项最接近。
方法二:特殊数字法,10.8%≈11%≈1/9,因此原式=35799亿×9≈3.6万亿×(10-1) =36万亿-3.6万亿=32.4万亿,对应B项。故正确答案为B。
例
(2017天津滨海新区)
据19世纪80年代初世界能源会议等组织的资料,世界煤资源地质储量为14.3万亿吨,其中探明储量为3.5万亿吨,约占24.5%;在总储量中硬煤占75%,褐煤占25%。
在世界煤炭总储量中,硬煤大约有:
A.9.84万亿吨 B.10.73万亿吨
C.3.58万亿吨 D.14.3万亿吨
【思路梳理】
题干未出现与时间有关的表述,则默认为与材料时间一致。题干求硬煤的值,对应材料找数据,“总储量中硬煤占75%”,根据在…中…的占比,可判定本题为现期比重问题。由在…中…的占比,后面为部分,前面为总体,可得总储量为总体,所求硬煤为部分,则本题可进一步梳理为已知总体和比重,求部分,代入公式部分=总体×比重求解即可。
解题步骤:
由文字材料第二行“其中”和“;”可知,探明储量是“其中”里的一部分,硬煤/褐煤和探明储量是并列关系,故总储量指的是世界煤资源地质储量。根据部分=总体×比重=14.3×75%=14.3×3/4=42.9/4=10+,对应B项。
故正确答案为B。
例
(2018山东)
2016年全年J省用新水量超过2亿立方米的5个行业用新水量合计19.1亿立方米,占总用新水量的67.6%,比重比上年下降0.9个百分点。
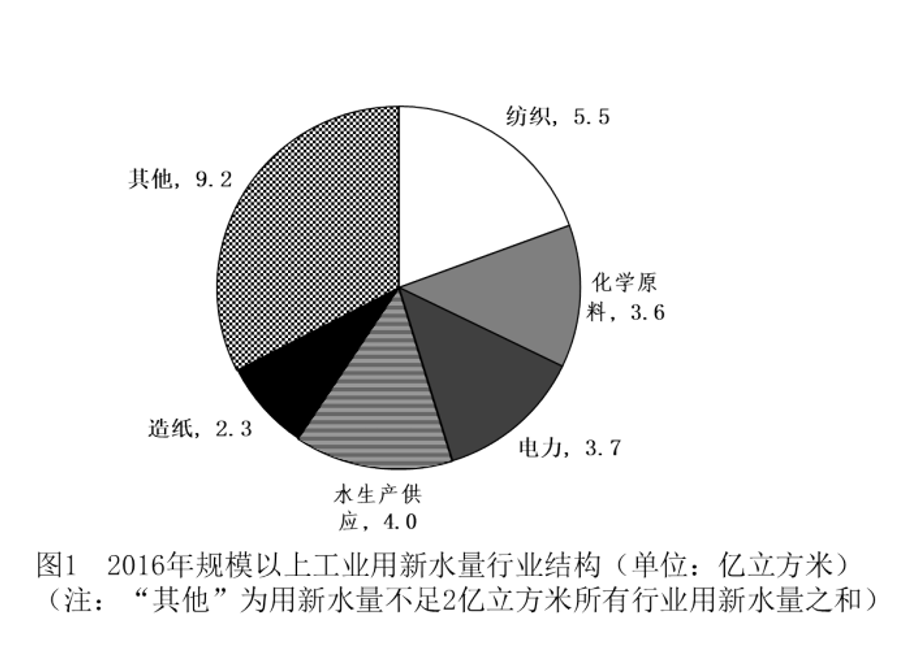
2016年J省用新水量最多的2个行业,用新水量占全省规模以上工业用新水总量的比重相差约多少个百分点?
A.5.3 B.6.7 C.7.9 D.9.5
【思路梳理】
根据题干“2016年······占······的比重”,结合材料时间为2016年,可判定本题为现期比重问题。本题需要先找到用新水量最多的2个行业,再将两个行业占全省的比重做差,若A行业和B行业分别为第1和第2的行业,则可列式为:A行业/全省-B行业/全省=(A行业-B行业)/全省。本题需要注意,注释中的内容:“其他”是不足2亿立方米的多个行业之和,故不能当做一个行业。
解题步骤:
方法一:定位图形材料可知,“用新水量超过2亿立方米的5个行业用新水量合计19.1亿立方米,占总用新水量的67.6%”,根据占前为部分,占后为总体,则部分/比重,则全省规模以上用新水总量=19.1/57.6%。故比重差值约等于5.3%,即5.3个百分点,与A项最接近。
方法二:定位文字材料第二段可知,全年用新水量超过2亿立方米的5个行业用新水量合计19.1亿立方米。定位图形材料可知,用新水量最多的2个行业为纺织业和水生产供应业,新水量分别为5.5亿立方米、4亿立方米,其他行业新水量为9.2亿立方米。故比重差值约等于5.3%,即5.3个百分点,与A项最接近。
方法三:定位图形材料可知,用新水量最多的2个行业为纺织业和水生产供应业,新水量分别为5.5亿立方米、4亿立方米,所以亿立方米,定位文字材料第二段可知,全年用新水量超过2亿立方米的5个行业用新水量为19.1亿立方米,占总用新水量的67.6%。那么1.91亿立方米,占总用新水量的6.76%,1.5亿立方米肯定小于6.76%,根据选项排除B、C、D,选A。
例
(2019山东)
2017年末,全国医疗卫生机构床位794.0万张,其中:医院612.0万张(占77.1%),基层医疗卫生机构152.9万张(占19.3%)。医院中,公立医院床位占75.7%,民营医院床位占24.3%。
2017年末公立医院床位数占全国医疗卫生机构床位数的比重为:
A.75.7% B.77.1%
C.58.4% D.56.2%
【思路梳理】
根据题干“2017年末…占…的比重”,结合材料时间也是2017年末,可判定本题为现期比重问题。根据占前为部分,占后为总体,可得公立医院床位数为部分量,全国医疗卫生机构床位数为总体量,材料中未直接给出公立医院床位数,但可根据部分=总体×比重求得。
解题步骤:
方法一:对应材料找数据,“医院中,公立医院床位占75.7%”,根据在…中…的占比,后面为部分,前面为总体,可得分子公立医院床位数为部分量,医院床位数为总体量,根据部分量=总体量×比重,则分子=医院床位数×比重,故所求=公立医院床位数/全国医疗卫生机构床位数=(医院床位数×比重)/全国医疗卫生机构床位数=(612×75.7%)/794,612/794<1,结果<75.7%,排除A、B项;75.7%看成 3/4,原式≈[612×(3/4)]÷794=1836/4÷794=459/794>459/800=57.X%,对应C项。
方法二: 所求=公立医院床位数/全国医疗卫生机构床位数=公立医院床位数/医院床位数*医院床位数/全国医疗卫生机构床位数=77.1%×75.7%≈77.1%×3/4,原式变为 231/4=57.X,将75.7%看成3/4是看小了,所以结果要比57.X%大,对应C项。
例
(2020安徽)
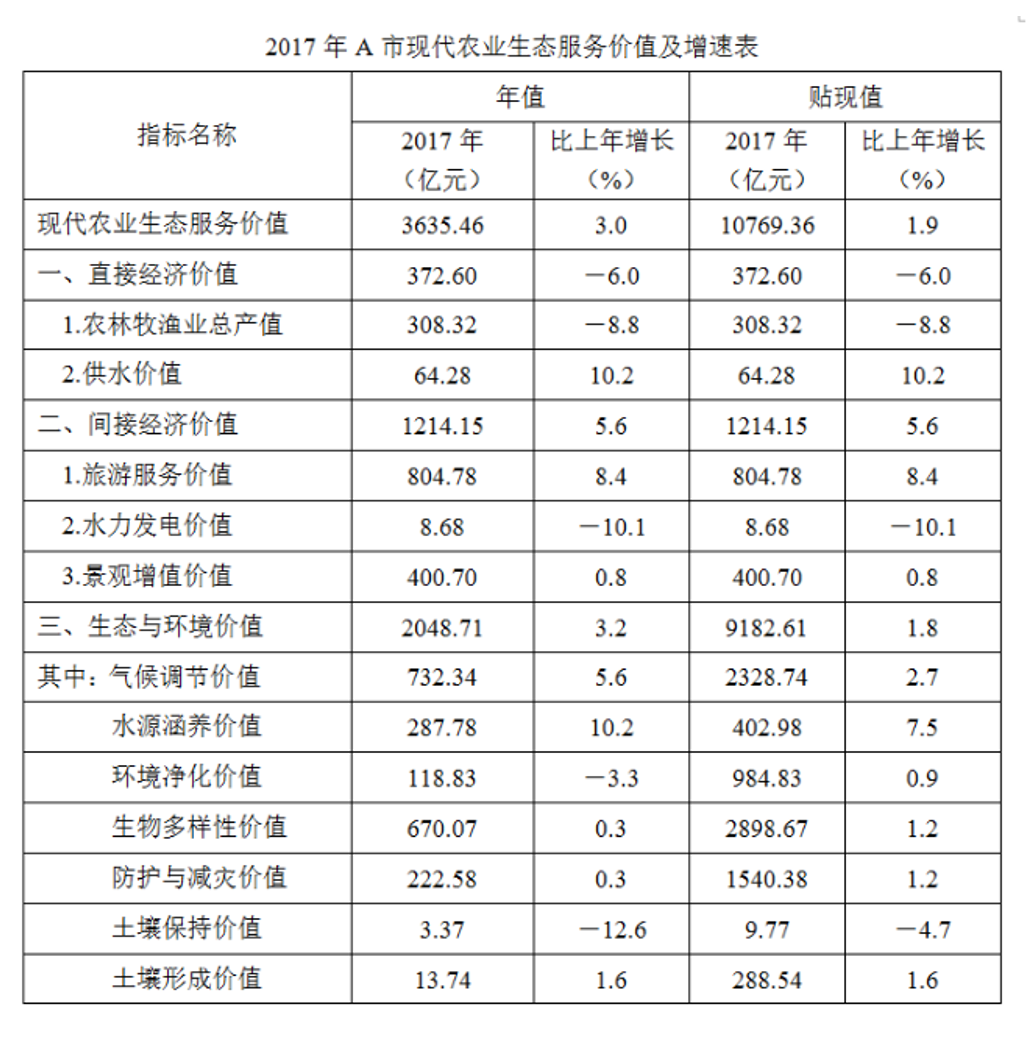
能够正确描述2017年A市间接经济价值年值中三个指标占比的统计图是:

A.A B.B C.C D.D
【思路梳理】
根据题干“2017年…占比…”,结合材料时间“2017年”,可判定本题为现期比重问题。由题干可得,间接经济价值年值三个指标分别为部分量,间接经济价值年值为总体量,可根据公式:比重=部分/总体,分别求出三个指标的占比,或根据三个占比间的关系,得出正确选项。
解题步骤:
方法一:定位表格材料可得:2017年间接经济价值年值为1214.15亿元,旅游服务价值年值为804.78亿元,水力发电价值年值为8.68亿元,景观增值价值年值为400.70亿元。旅游服务价值年值占比为2/3,即大于、小于,说明第一个扇形的圆心角大于180°、小于1/2,小于3/4,说明第一个扇形的圆心角大于180°小于270,结合选项排除B、C两项;景观增值价值年值占比大于1/4,说明最后一个扇形的圆心角大于90°,结合选项排除D项,A当选。
方法二:旅游服务价值年值与景观增值价值年值比例约为2,说明第一个扇形的面积约为第三个扇形面积的2倍,结合选项可排除B、C、D项;A当选。
(三)粉笔小拓展
(1)若题干没有给明具体时间,则默认为所求时间与材料所给时间一致,即所求时间为现期,如例3。
(2)若总体相同,求比重差(和),可以用部分量的差(和)直接除以总体,如例4。
(3)求现期比重时,若所求的部分量或总体量未直接给出,而是以比重的形式给出,可观察材料中,是否存在第三量与所求的部分量和总体量都有比重关系,若有可利用比重的传递,直接用两个比重的乘积求解,如例5。
注:结论推导:A/C=A/b*B/C=比重1比重2(A为所求的部分量;B为与A、C有比重关系的量;C为所求的总体量。)
(4)比重问题中,若出现饼形图(如例6),可以有以下技巧:
1.构图原则:12点钟方向,根据材料数据依次按顺时针排布。
2.方法:
(1)有总体;先看部分与整体的比例关系(特殊值:1/2,1/4,3/4 ,90°对应1/4圆;180°对应1/2圆;270°对应3/4圆)。
(2)无总体:先看最大、最小,再看内部倍数关系。
02
基期比重
(一)必备知识
1.题型特征
(1)所求时间在材料所给时间之前;
(2)关键字“占”:求 A 占 B 的比重,或 B 中 A 的占比。
注:A 代表部分量、B 代表整体量
2.计算公式
基期比重=A/B*(1+b)/(1+a)(A表示现期部分量,B表示现期总体量,a:分子的增长率,b:分母的增长率)。
3.公式推导
根据基期量=现期量/1+增长率可知部分基期量=A/(1+a)、基期总量=B/(1+b),则基期比重等于A/B*(1+b)/(1+a)。
4.解题思路
若材料中已知 A、B 的现期量和增长量,可根据公式:基期量=现期量-增长量,计算出 A、B 的基期量,再用公式:比重=A/B。
若材料中已知 A、B 的现期量和对应增长率 a、b,则根据基期比重公式A/B*(1+b)/(1+a):
(1)先利用截位直除,计算A/B;
(2)再根据1+b/1+a来判定大小。
① 如果1+b/1+a大于1,则基期比重大于A/B;
② 如果1+b/1+a小于1,则基期比重小于A/B;
③ 如果只能排除部分选项,则可用截位直除估算1+b/1+a的值。
(二)典型考法与解题思路
例
(2019联考)
2017年上半年,全国居民人均可支配收入12932元,比上年同期名义增长8.8%,其中,城镇居民人均可支配收入18332元,增长8.1%(以下如无特别说明,均为同比名义增长);农村居民人均可支配收入6562元,增长8.5%。按收入来源分,2017年上半年,全国居民人均工资性收入7435元,增长8.6%,占全国居民人均可支配收入的比重为57.5%。
2016年上半年,全国居民人均工资性收入占全国居民人均可支配收入的比重约为:
A.53.6% B.57.6%C.60.6% D.63.6%
【思路梳理】
根据题干“2016年上半年…占…的比重”,结合材料时间“2017年上半年”,可判定本题为基期比重问题。将材料数据代入基期比重公式A/B*(1+b)/(1+a)求解即可,但要注意观察,材料中是否已给出现期比重,若给出,直接比较1+b/1+a与1的关系。
解题步骤:
定位文字材料 “2017年上半年,全国居民人均可支配收入12932元,比上年同期名义增长8.8%”… 2017年上半年,全国居民人均工资性收入7435元,增长8.6%,占全国居民人均可支配收入的比重为57.5%”,代入基期比重公式A/B*(1+b)/(1+a),则结果略大于57.5%,对应B项。
例
(2018国考)
2018年我国全年研究与试验发展(R&D)经费支出19657亿元,比上年增长11.6%,与国内生产总值之比为2.18%,其中基础研究经费1118亿元。全年国家重点研发计划共安排1052个项目,国家科技重大专项共安排563个课题,国家自然科学基金共资助44504个项目。截至年底,正在运行的国家重点实验室501个,累计建设国家工程研究中心132个,国家工程实验室217个,国家企业技术中心1480家。国家科技成果转化引导基金累计设立21支子基金,资金总规模313亿元。全年境内外专利申请432.3万件,比上年增长16.9%;授予专利权244.7万件,增长33.3%;PCT专利申请受理量为5.5万件。截至年底,有效专利838.1万件,其中境内有效发明专利160.2万件,每万人口发明专利拥有量11.15件。全年共签订技术合同41.2万项,技术合同成交金额17697亿元,比上年增长31.8%。
2017年专利授予件数占境内外专利申请件数的百分比是
A.47.4% B.49.6% C.50.3% D.56.6%
【思路梳理】
根据题干“2017年…占…的百分比是…”,结合文字材料时间 “2018年”,可判定本题为基期比重问题。将材料数据代入基期比重公式求解即可。
解题步骤:
定位文字材料“全年境内外专利申请432.3万件,比上年增长16.9%;授予专利权244.7万件,增长33.3%”。 代入基期比重公式=A/B*(1+b)/(1+a)=49.6%。
(三)粉笔小拓展
在计算基期比重问题之前,要注意看下现期比重在资料中是否已给出,若给出可直接使用,以节省做题时间,如例7。
03
两期比重比较
(一)必备基础知识
1.题型特征
题干出现两个时间及“占”,需要判断上升或下降。
2.计算公式
两期比重差=A/B*(a-b)/(1+a)(A表示现期部分量,B表示现期总体量,a:分子的增长率,b:分母的增长率)。
3.公式推导
两期比重差=现期比重-基期比重=A/B*(a-b)/(1+a)
4.解题思路(口诀):
(1)a>b,比重上升。
(2)a<b,比重下降。
(3)a = b,比重不变。
注:a 为分子(部分量)的增长率,b 为分母(总体量)的增长率。
(二)典型考法与解题思路
例
2018年前三季度,S省社会物流总额35357.26亿元,同比增长6.4%,增速比上半年放缓0.7个百分点。其中,工业品物流总额16636.15亿元,同比增长0.2%,增速比上半年放缓2.1个百分点;外部流入(含进口)货物物流总额17357.31亿元,同比增长12.1%,增速比上半年加快0.8个百分点;农产品物流总额875.06亿元,同比增长11.6%,增速比上半年加快0.5个百分点;单位与居民物品物流总额457.86亿元,同比增长40.7%,增速比上半年放缓3个百分点;再生资源物流总额30.88亿元,同比下降7.0%,降幅比上半年扩大4.3个百分点。
在工业品物流、外部流入(含进口)货物物流、农产品物流、单位与居民物品物流和再生资源物流中,2018年前三季度物流总额占社会物流总额的比重高于上年水平的有几类?
A.4 B.3 C.2 D.1
【思路梳理】
根据题干所求“2018年前三季度…占…比重高于上年水平的有几类”,可判定本题为两期比重比较问题。本题求比重高于上年,即 a>b。故只需找到2018年前三季度物流总额的增长率高于全国社会物流总额增长率的类别分别有哪些,再将类别数求和即可得出正确选项。
解题步骤:
根据两期比重比较的结论:当部分增长率a>总体增长率b时,可判定比重上升。定位文字材料第一段“2018年前三季度,S省社会物流总额35357.26亿元,同比增长6.4%。其中,工业品物流…同比增长0.2%;外部流入(含进口)货物物流…同比增长12.1%;农产品物流…同比增长11.6%;单位与居民物品物流…同比增长40.7%;再生资源物流…同比下降7.0%”。即总体增长率b=6.4%,其中满足“部分增长率a>b(6.4%)”的有:外部流入(含进口)货物物流(12.1%)、农产品物流(11.6%)、单位与居民物品物流(40.7%),共3类。
故正确答案为B。
(三)粉笔小拓展
在比较 a、b 的大小时,由于是增长率的比较,故需带正负号。
04
两期比重计算
(一)必备基础知识
1.题型特征
题干出现两个时间+比重,问上升(下降)几个百分点。
2.计算公式
两期比重差=A/B*(a-b)(1+a)(A表示现期部分量,B表示现期总体量,a:分子的增长率,b:分母的增长率)。
3.解题思路
(1)判升降:a>b,上升;a<b,下降;a = b,不变。
(2)定大小:小于|a-b|,即比重差<增速差的绝对值。
注:a 为分子(部分量)的增长率,b 为分母(总体量)的增长率
(二)典型考法与解题思路
例
(2018山东)
2016年,J省规模以上工业取水量为86.4亿立方米,比上年增长4.4%。其中,直接采自江、河、淡水湖、水库等的地表淡水68.1亿立方米,比上年增长3.8%,所占比重比上年下降0.4个百分点;自来水取水量15.9亿立方米,同比增长6.0%。
J省2016年规模以上工业自来水取水量占总取水量的比重比上年:
A.提高0.3个百分点 B.下降0.3个百分点
C.提高4个百分点 D.下降4个百分点
【思路梳理】
题目出现“…占…比重比上年”,选项为提高/下降…个百分点,判定本题为两期比重计算问题。材料分别给出J省2016年规模以上工业自来水取水量和J省规模以上工业取水量的同比增速,则先判方向,根据a与b的大小关系,排除两个选项;再定大小,根据比重差<增速差 的绝对值得出正确选项。
解题步骤:
(1)判方向:工业自来水取水量为a,总取水量为b。定位材料可得,规模以上工业自来②水取水量增长率a=6.0%,总取水量增长率b=4.4%,a>b,比重上升,排除B、D项。
(2)定大小:比重差<1.6%,排除C项,对应A项。
故正确答案为A。
(三)粉笔小拓展
定大小的技巧:
(1)若只有一个选项满足比重差<增速差的绝对值,直接选即可。
(2)若有多个选项满足比重差<增速差的绝对值,时间不充足直接猜最小的选项即可,但这种“猜”的技巧有较小的风险。因此,如果时间充足可代入公式:A/B*(a-b)/(1+a),利用截位直除进行速算。
通过对上述理论知识的学习,小粉笔相信考生们已经掌握了比重问题理论知识和解题技巧,建议考生们后续多多练习加以巩固哦!成功不是将来才有的,而是从决定去做的那一刻起,持续累积而成。小粉笔期待见证你的高光时刻!
