说到数学问题，它应该让很多小伙伴都很头疼。不用担心！小粉笔帮忙整理了数量关系里常见的几种问题类型和公式，搭配真题习题，助你一臂之力！快来看看吧！
▎一、行程问题
（一）普通行程
公式：路程=速度×时间（S=V×T）
平均速度=总路程÷总时间
等距离平均速度=
真题示例1
【2018国考】一辆汽车第一天行驶了5个小时，第二天行驶了600公里，第三天比第一天少行驶200公里，三天共行驶了18个小时。已知第一天的平均速度与三天全程的平均速度相同，问三天共行驶了多少公里？
A. 800
B. 900
C. 1000
D. 1100
【解析】设第一天的平均速度为v，则第一天路程为5v，第三天路程为5v-200。由全程平均速度与第一天相同，可得方程：5v+600+5v-200=18v，解得v=50，则三天共行驶18×50=900公里。
故正确答案为B。
【分析】总路程=总时间×平均速度为基本公式的变形。
真题示例2
【2019江苏】警校某班学生分两个小组在甲、乙两地间进行野外负重拉练。已知去程两个小组的速度分别是5千米/小时、4千米/小时，返程两个小组的速度都下降了20%。若两个小组的出发时间相差54分钟，但同时返回到出发点，则甲、乙两地间的距离是
A. 20千米
B. 16千米
C. 12千米
D. 8千米
【解析】根据题意，两个小组返程速度为5×（1-20%）=4千米/小时，4×（1-20%）=3.2千米/小时。由于往返路程不变，故可套用等距离平均速度公式（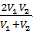
），则两个小组往返甲、乙两地的平均速度分别为
千米/小时，
千米/小时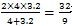。由于第二组速度慢，所以第二组比第一组多用54分钟，即
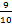小时。设甲、乙两地之间往返的距离为S，则9/10=s/32/9-s/40/9，解得S=16千米，故甲、乙两地的距离为：16÷2=8千米。
故正确答案为D。
【分析】题干中出现同一路程往返，可利用等距离平均速度公式计算出平均速度。
（二）相对行程
公式：相遇追及
真题示例1
【2018联考】甲、乙、丙、丁四人同时同地出发，绕一椭圆形环湖栈道行走。甲顺时针行走，其余三人逆时针行走。已知乙的行走速度为60米/分钟，丙的速度为48米/分钟。甲在出发6、7、8分钟时分别与乙、丙、丁三人相遇，求丁的行走速度是多少？
A. 31米/分钟
B. 36米/分钟
C. 39米/分钟
D. 42米/分钟
【解析】由题意可知，甲与乙相遇，甲与丙相遇均为两人合走完一个环湖的全程。根据总路程相等，可得方程（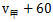
）×6=（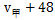
）×7，解方程得
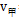=24米/分钟。同理，甲与乙相遇，甲与丁相遇时的路程也相等，（24+60）×6=（24+
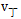）×8，解得
=39米/分钟。
故正确答案为C。
【分析】题干出现“相遇”即相遇问题，找
和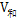
。
真题示例2
【2019国考】甲车上午8点从A地出发匀速开往B地，出发30分钟后乙车从A地出发以甲车2倍的速度前往B地，并在距离B地10千米时追上甲车。如乙车9点10分到达B地，问甲车的速度为多少千米/小时？
A. 30
B. 36
C. 45
D. 60
【解析】设甲车的速度为v千米/小时，乙车的速度为甲车的2倍即2v千米/小时。甲车出发30分钟即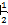
小时后乙车开始追，则两车的路程差为
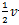千米，由追及公式“路程差=速度差×追及时间”可得，追及时间=
小时。乙车在上午8点的30分钟后出发，9点10分到达B地，共用时9:10-8:30=40分钟=
小时。设乙在C点追上甲，则CB=10千米，乙车从C地到B地用时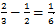
小时。则乙车的速度=
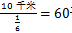千米/小时，甲车的速度=60÷2=30千米/小时。
故正确答案为A。
【分析】题干中出现“追上”即追及问题，找到找
和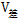
。
▎二、经济利润问题
（一）基础经济
公式：利润=售价-进价；利润率=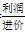
；折扣=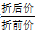
；总价=单价×个数。
真题示例
【2018联考】某苗木公司准备出售一批苗木，如果每株以4元出售，可卖出20万株，若苗木单价每提高0.4元，就会少卖10000株。问在最佳定价的情况下，该公司最大收入是多少万元？
A. 60
B. 80
C. 90
D. 100
【解析】假设在原价基础上提价x次，则共提高0.4x元，少卖了10000x株，即x万株。根据题意可得方程，收入y=（4+0.4x）×（20-x），令y=0，解得x1=-10，x2=20，当x=
=5时，y取得最大值=（4+0.4×5）×（20-5）=90万元。
故正确答案为C。
【分析】问题问“收入”，代入公式：收入=单价×销量。
（二）分段计费
真题示例
【2018江西】为了节约水资源，某城市规定每人每月不超过5吨，则按2.5元/吨收费；超出5吨的，超出部分按4元/吨收费，每次收费时用水量都按整数计算，已知胡家3口人，熊家4口人。某月月底结算时，胡家收费69.5元，比熊家多交了15.5元。那么，熊家该月用了多少吨水？
A. 20
B. 21
C. 22
D. 23
【解析】熊家该月收费69.5-15.5=54元。设熊家该月用了x吨水，根据总收费为两部分的和可得方程2.5×5×4+（x-5×4）×4=54。解方程得x=21吨。
故正确答案为B。
【分析】题干中出现“不超过5吨”，“超出5吨”，分段计算，汇总求和。
▎三、容斥原理
（一）两集合
公式：A+B-都满足=总数-都不满足
真题示例
【2018联考】某试验室通过测评Ⅰ和Ⅱ来核定产品的等级：两项测评都不合格的为次品，仅一项测评合格的为中品，两项测评都合格的为优品。某批产品只有测评Ⅰ合格的产品数是优品数的2倍，测评Ⅰ合格和测评Ⅱ合格的产品数之比为6：5。
若该批产品次品率为10%，则该批产品的优品率为：
A. 10%
B. 15%
C. 20%
D. 25%
【解析】假设这批产品的优品数为x，则只有测评Ⅰ合格的产品数为2x，测评Ⅰ合格的全部产品数为x+2x=3x，测评Ⅱ合格的产品数为
×3x=2.5x。根据两集合容斥原理公式：A+B-都满足=总数-都不满足，则这批产品非次品数量为3x+2.5x-x=4.5x，在总数中占比为1-10%=90%，则产品总数为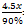
=5x，则优品率为
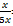=20%。
故正确答案为C。
【分析】题干中出现测评Ⅰ和Ⅱ即两集合，没有具体数，赋值。
（二）三集合
公式：A+B+C-AB-AC-BC+ABC=总数-都不满足（标准）
A+B+C-满足两项-2×满足三项=总数-都不满足（非标准）
满足一项+满足两项+满足三项=总数-都不满足
真题示例1
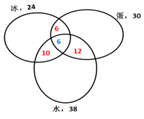
【2018联考】联欢会上，有24人吃冰激凌、30人吃蛋糕、38人吃水果，其中既吃冰激凌又吃蛋糕的有12人，既吃冰激凌又吃水果的有16人，既吃蛋糕又吃水果的有18人，三样都吃的则有6人。假设所有人都吃了东西，那么只吃一样东西的人数是多少？
A. 12
B. 18
C. 24
D. 32
【解析】如图所示，共有24人吃冰淇淋，其中有12人吃了蛋糕，16人吃了水果，既吃了蛋糕又吃了水果的有6人，则只吃了冰淇淋的人数为24-（16+12-6）=2人；同理，只吃了蛋糕的人数为30-（12+18-6）=6人；只吃了水果的人数为38-（16+18-6）=10人，则只吃一样东西的人数为2+6+10=18人。
故正确答案为B。
【分析】题干中出现了三类食品即三个集合，问“只吃一样”，画图。
真题示例2
【2018江西】某高校做有关碎片化学习的问卷调查，问卷回收率为90%，在调查对象中有180人会利用网络课程进行学习，200人利用书本进行学习，100人利用移动设备进行碎片化学习，同时使用三种方式学习的有50人，同时使用两种方式学习的有20人，不存在三种方式学习都不用的人。那么，这次共发放了多少份问卷？
A. 370
B. 380
C. 390
D. 400
【解析】设共发放问卷x份，根据容斥原理三集合非标准型公式：A+B+C-满足两项-2×满足三项=总数-都不满足，180+200+100-20-2×50=90%x-0，解得x=400份。则这次共发放了400份问卷。
故正确答案为D。
【分析】题干中出现了三种方式即三个集合，“同时使用两种”代入非标准公式。